| 年级 | 科目 | 问题描述 | 提问时间 |
| 初二 | 数学 | 数学 | 2014-05-12 21:30:15 |
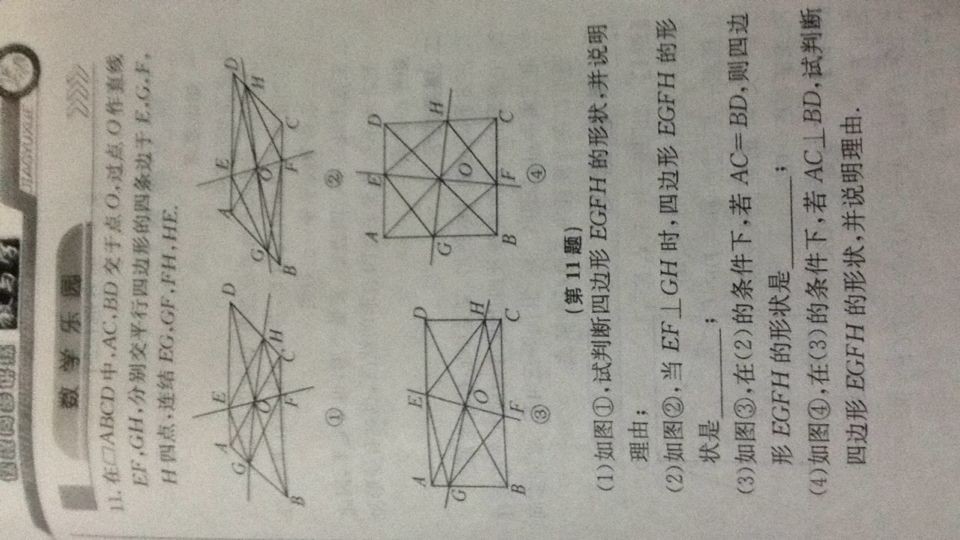 | |||
| 王老师 2014-05-12 21:42:23 | |||
(1)由于平行四边形对角线的交点是它的对称中心, 即可得出OE=OF、OG=OH;根据对角线互相平分的四边形
是平行四边形即可判断出EGFH的性质;
故四边形EGFH是菱形;
故结论同(2); 则对角线相等且互相垂直平分;可通过证△BOG≌△COF, 得OG=OF,从而证得菱形的对角线相等, 根据对角线相等的菱形是正方形即可判断出EGFH的形状. | |||
| 王老师 2014-05-12 21:42:58 | |||
解:(1)四边形EGFH是平行四边形
证明:∵▱ABCD的对角线AC、BD交于点O, | |||
| 王老师 2014-05-12 21:43:23 | |||
| (2)∵四边形EGFH是平行四边形,EF⊥GH, ∴四边形EGFH是菱形; (3)菱形; | |||
| 王老师 2014-05-12 21:44:07 | |||
四边形EGFH是正方形
证明:∵AC=BD, | |||