| 年级 | 科目 | 问题描述 | 提问时间 |
| 高二 | 数学 | 数学导数问题 | 2016-04-04 10:38:39 |
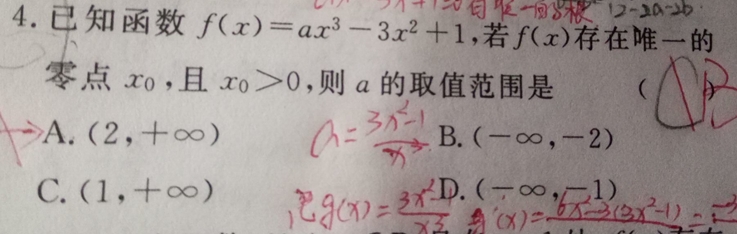 | |||
| 学点点顾老师 2016-04-04 11:15:12 | |||
 | |||
| 学点点顾老师 2016-04-04 11:15:25 | |||
对原函数求导,f'(x)=x(3ax-6),易知 1)当a>0时,原函数在(-无穷,0)递增,(0,2/a)递减,(2/a,无穷)递增。又因为原函数当x等于0时等于f(0)=1,且当x趋近负无穷时值为无穷,必有一个负的零点,与题目矛盾。 2)a小于0时,原函数在(-无穷,a/2)递减,(a/2,0)递增,(0,无穷)递减。且f(0)=1所以在(0,无穷)上必有零点。只要满足当x=a/2是函数大于0就成立,接f(a/2)>0可得a的范围是(负无穷,-2) | |||