| 年级 | 科目 | 问题描述 | 提问时间 |
| 初二 | 数学 | 三角形 | 2014-04-19 08:44:49 |
| 如图 在三角形abc中,AB=AC ,AD是BC边上的高,点M时AD的中点,直线MC交AB于点P,求证,AP=三分之一AB。 | |||
| 王老师 2014-04-19 09:14:20 | |||
证明:过点D作DN平行BA交CP于N 所以DN/BP=DC/BC 角PAM=角MDN 角APM=角MNP 所以三角形APM和三角形DNM相似(AA) 所以AP/DN=AM/DM 因为点M是AD的中点 所以AM=DM 所以AP=DN 所以AP/BP=CD/BC 因为AB=AC 所以三角形ABC是等腰三角形 因为AD是三角形ABC的高 所以AD是等腰三角形ABC的中线 所以BD=CD=1/2BC 所以AP/BP=1/2 因为AP+BP=AB 所以AP/AB=1/3 AP=1/3AB | |||
| 王老师 2014-04-19 09:15:05 | |||
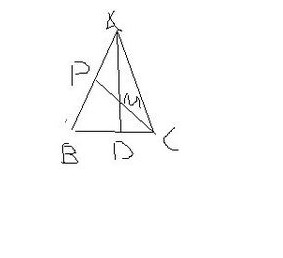 | |||