| 年级 | 科目 | 问题描述 | 提问时间 |
| 初二 | 数学 | 反证法 | 2014-04-19 08:30:32 |
| 如图所示,在三角形ABC中,AB>AC,AD是内角平分线,AM是BC边上的中线,求证,点M不在线段CD上。 用反证法 | |||
| 王老师 2014-04-19 09:16:01 | |||
| 假设点M不在线段CD上不成立,则点M在线段CD上. 延长AM到N,使AM=MN,连接BN; 在△AMC和△NMB中, BM=CM,∠AMC=∠BMN,AM=MN, ∴△AMC≌△NMB(SAS); ∴∠MAC=∠MNB,BN=AC; 根据M在线段CD上,则∠BAM>∠MAC, ∴∠MNB<∠BAM, ∴BN>AB, 即AC>AB;与AB>AC相矛盾. 因而M在线段CD上是错误的. 所以点M不在线段CD上. | |||
| 王老师 2014-04-19 09:16:42 | |||
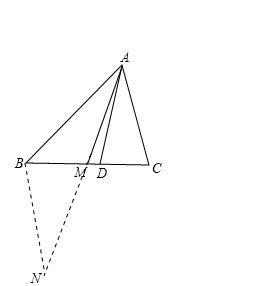 | |||
| 姜璠 2014-04-19 15:25:16 | |||
| 谢谢老师啊 | |||