| 年级 | 科目 | 问题描述 | 提问时间 |
| 初一 | 数学 | 数学应用题 | 2014-03-03 20:52:30 |
 | |||
| 王老师 2014-03-03 21:00:00 | |||
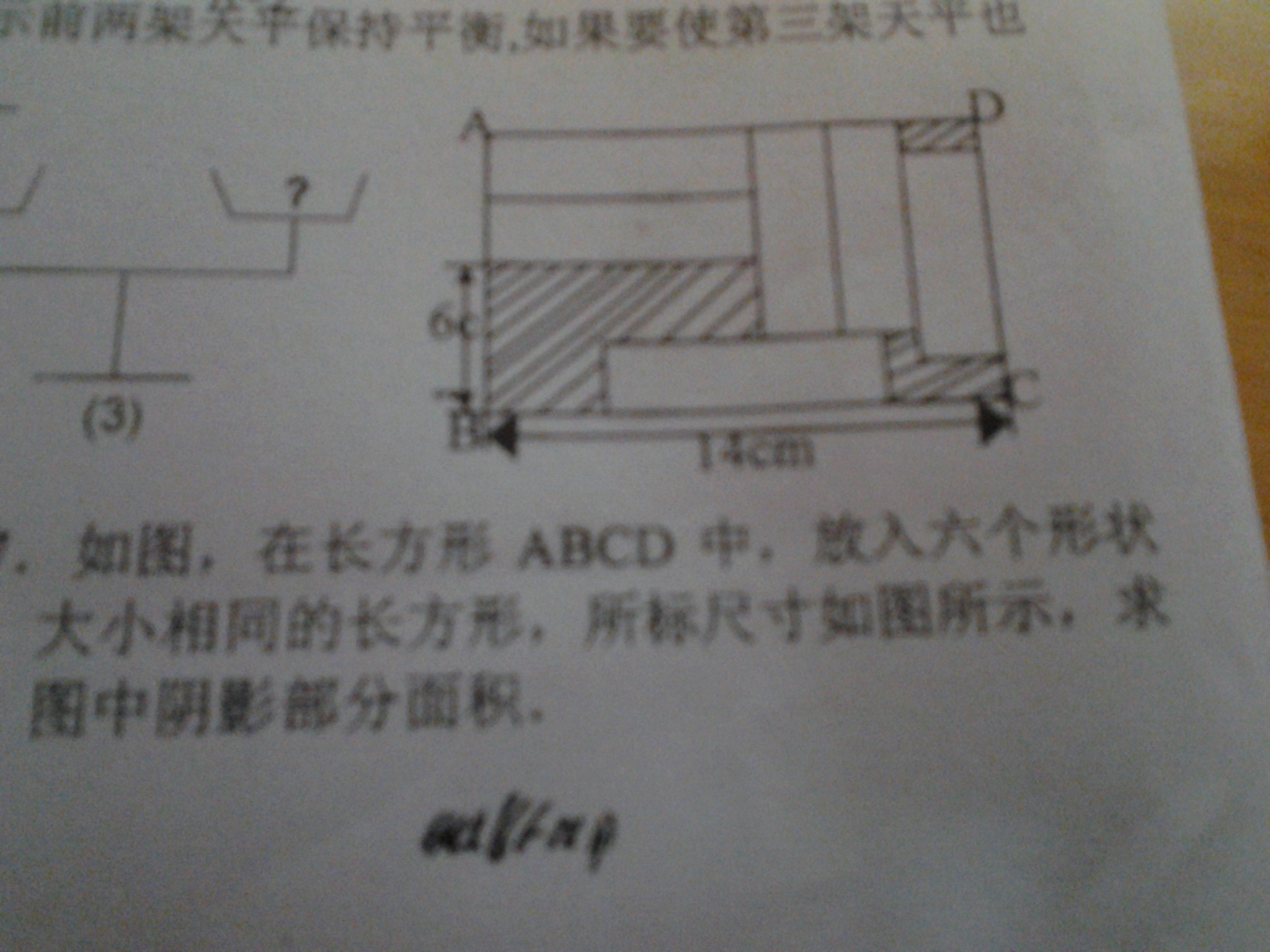
设长方形的长和宽为未数,根据图示可得到关于xy的两个方程, 可求得解,从而可得到大长方形的面积, 再根据阴影部分的面积 =大长方形的面积-6个小长方形的面积求解即可. | |||
| 王老师 2014-03-03 21:00:38 | |||
| 解:设小长方形的长为x,宽为y,如图可知, x+3y=14,① x+y-2y=6,即x-y=6,② ①-②得4y=8,y=2,代入②得x=8, 因此,大矩形ABCD的宽AD=6+2y=6+2×2=10. 矩形ABCD面积=14×10=140(平方厘米), 阴影部分总面积=140-6×2×8=44(平方厘米) | |||