| 年级 | 科目 | 问题描述 | 提问时间 |
| 初三 | 数学 | 圆 | 2014-02-21 21:20:33 |
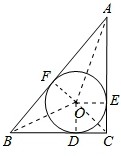
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,其内切圆○I分别切BC,AC,CB于点D,E,F. (1)试说明:○I的半径r=1/2(a+b-c) (2)若BD和AE是方程x²-5x+6的两个根(BD<AE),求△ABC的三边长 (3)在(2)的条件下,求△ABC的内切圆与外切圆的圆心距
| |||
| 王老师 2014-02-22 09:48:36 | |||
| 分别连接OA、OB、OC、OD、OE、OF ∵⊙O是△ABC内切圆,D、E、F为切点, ∴CD=CE,AE=AF,BD=BF,∠OEC=∠ODC=Rt∠, ∵∠C=Rt∠,CD=CE, ∴四边形CDOE是正方形, ∴CD=CE=r,AE=b-r=AF,BD=a-r=BF, ∵BF+AF=AB=c, ∴(a-r)+(b-r)=c,
∴r=1/2(a+b-c) | |||
| 王老师 2014-02-22 10:00:52 | |||
 | |||