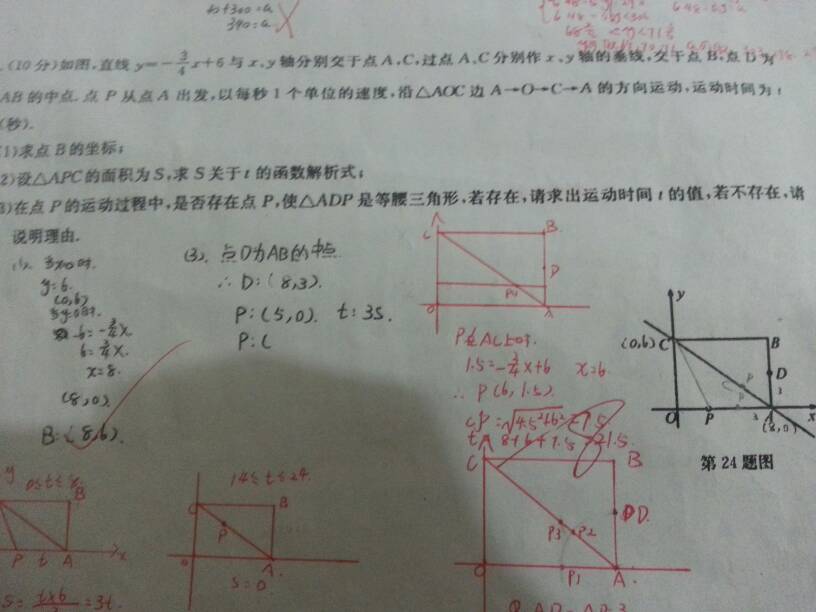
（1）直线y=-3x/4+6与x轴交点A(8，0）；与y轴交点C（0,6）
矩形ABCO中：AO=BC=8；OC=AB=6；AC=√(8^2+6^2)=10.
所以：点B的坐标为（8,6）。
（2）
当点P在A-O上运动时，点P为（8-t，0），

t<=8；S=AP*CO/2=t*6/2=3t；
当点P在O-C上运动时，点P为（0，t-8），

8<=t<=14；S=PC*AO/2=[6-(t-8)]*8/2=56-4t；
当点P在C-A上运动时，A、P和C三点共线，14<=t<=24；S=0
所以：
0<=t<=8，S=3t；
8<=t<=14，S=56-4t；
14<=t<=24，S=0
（3）因为：点D是AB的中点，

所以：AD=AB/2=6/2=3，点D为（8,3）
3.1）点P在AO上时，三角形APD是直角三角形，

只能是AP=AD：t=3；
3.2）点P在OC上时，如果点P在AD的垂直平分线y=AD/2=3/2上时，

PA=PD：t-8=3/2，t=19/2；
3.3）点P在CA上时：
点P坐标为x=PCcos∠OAC=(t-14)*(8/10)=(4t-56)/5；
y=6-PC*sin∠OAC=6-(t-14)*(6/10)=(72-3t)/5。
3.3.1）点P在AD的垂直平分线上y=3/2，PA=PD，

(72-3t)/5=3/2，t=43/2；
3.3.2）PD=AD时，点D在AP的垂直平分线上y-3=4(x-8)/3

即y=4x/3-23/3，与AC直线y=-3x/4+6联立解得AP的中点为（164/25,25/25）
所以：(4t-56)/5+8=2*164/25，t=102/5
3.3.3）PA=AD时，8+6+10-t=3，t=21
综上所述，当t=3或者t=19/2或者t=43/2

或者t=102/5或者t=21时，三角形ADP为等腰三角形。