| 年级 | 科目 | 问题描述 | 提问时间 | |
| 初三 | 数学 | 数学 | 2013-12-19 21:09:24 | |
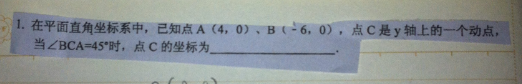 | ||||
| 沈艺柔 2013-12-20 09:41:41 | ||||
| 分析:如解答图所示,构造含有90°圆心角的⊙P,则⊙P与y轴的交点即为所求的点C. 注意点C有两个.
解:设线段BA的中点为E, AB=5,则易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=5根号2
以P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C, ∴OC=OF+CF=5+7=12 ∴点C坐标为(0,12);
(2)如答图2所示,在第3象限可以参照(1)作同样操作,同理求得y轴负半轴上的点C坐标为(0,-12). | ||||