学点点

详细内容

疑难解答：

学员在学习中遇到问题，在这里能得到及时的解决。有问题随时提问，老师解答及时，不留学习盲点。有不懂的题目问老师，逐渐养成独立解决问题的能力。

年级

科目

问题描述

提问时间

初二

数学

2014-09-26 20:42:48

余雯馨老师 2014-09-26 20:45:03

△EMC的形状是等腰直角三角形，
理由是：
连接AM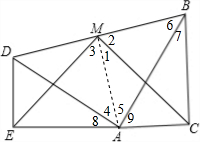，菁优网

∵∠8=30°，∠9=60°，
∴∠DAB=180°-30°-60°=90°，
∵M为BD中点，AD=AB（已知两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起），
∴AM⊥BD（等腰三角形底边的高也平分底边）
AM=BM=DM（直角三角形斜边上中线等于斜边的一半）
∴∠5=∠6=1/2（180°-90°）=45°，∠4=∠BDA=45°，
∵∠7=30°，
∴∠MBC=45°+30°=75°，
同理∠MAE=75°=∠MBC，
在△BCM和△AEM中

BM=AM

∠MBC=∠MAE

BC=AE

，
∴△BCM≌△AEM（SAS），
∴EM=CM，∠3=∠2，
∵AM⊥BD，
∴∠1+∠2=90°，
∴∠1+∠3=90°，
∴△EMC是等腰直角三角形．

该问题已结帖