学点点

详细内容

疑难解答：

学员在学习中遇到问题，在这里能得到及时的解决。有问题随时提问，老师解答及时，不留学习盲点。有不懂的题目问老师，逐渐养成独立解决问题的能力。

年级	科目	问题描述	提问时间
初三	数学	5	2014-09-16 21:13:36

余雯馨老师 2014-09-16 21:20:43
（1）AD=CF．理由如下：在正方形ABCO和正方形ODEF中，AO=CO，OD=OF，∠AOC=∠DOF=90°， ∴∠AOC+∠COD=∠DOF+∠COD，即∠AOD=∠COF，在△AOD和△COF中， AO=CO ∠AOD=∠COF OD=OF ， ∴△AOD≌△COF（SAS）， ∴AD=CF；（2）与（1）同理求出CF=AD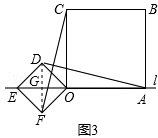，如图，连接DF交OE于G，则DF⊥OE，DG=OG= 12‍ OE， ∵正方形ODEF的边长为√2‍ ， ∴OE= √2‍ ×√2‍ =2， ∴DG=OG= 12‍ OE=12‍ ×2=1， ∴AG=AO+OG=3+1=4，在Rt△ADG中，AD= √AG²+DG²=√4‍²+1² =√17‍ ， ∴CF=AD=√17‍ ．
马卓怡 2014-09-16 22:57:56
‍ 是什么