| 年级 | 科目 | 问题描述 | 提问时间 |
| 初一 | 数学 | 数学 | 2014-08-26 22:40:56 |
 | |||
| 学点点闵老师 2014-08-26 22:53:59 | |||
| 分析:(1)延长AP交NB于点C,先根据平行线的性质求出∠MAP=∠ACB,再由三角形外角的性质即可求出答案; (2)先根据MA∥NB求出∠1=∠MAP,再由三角形外角的性质即可解答; (3)当P在MA与NB外部时,过点P作PD∥AB,根据两直线平行,同旁内角互补可求出∠APB+∠MAP+∠NBP=360°. | |||
| 学点点闵老师 2014-08-26 22:54:29 | |||
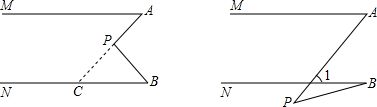 | |||
| 学点点闵老师 2014-08-26 22:54:50 | |||
| 解:(1)能. 延长AP交NB于点C. ∵MA∥NB, ∴∠MAP=∠ACB, ∵∠APB=∠ACB+∠NBP, ∴∠APB=∠MAP+∠NBP;(4分) (2)∵MA∥NB,∴∠MAP=∠1, ∵∠1是△PBD的外角, ∴∠1=∠APB+∠NBP, ∴∠APB=∠MAP-∠NBP;(2分) 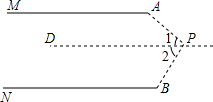 (3)如图所示,MA∥NB,可知∠APB+∠MAP+∠NBP=360°. 过P作PD∥MA,则∠1+∠MAP=180°,∠2+∠NBP=180°, ∴∠1+∠MAP+∠2+∠NBP=360°, ∴∠APB+∠MAP+∠NBP=360°. | |||