| 年级 | 科目 | 问题描述 | 提问时间 |
| 初二 | 数学 | 数学 | 2017-09-12 20:23:16 |
| 如图,点o是三角形ABC里的任意一点. 求证:角BOC=角A+角ABO+角ACO. 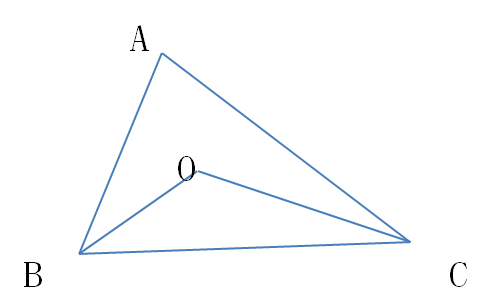 | |||
| 邹金 2017-09-12 20:28:05 | |||
填加辅助线!
| |||
| 学点点涂老师 2017-09-12 20:51:13 | |||
| ∠obc=∠abc-∠abo 1 ∠ocb=∠acb-∠aco 2 ∠obc+∠ocb=∠abc-∠abo+∠acb-∠aco 1+2 180-[∠obc+∠ocb]=180-∠abc+∠abo-∠acb+∠aco 180同时先去2边 所以 ∠OBC=∠A+∠ABO+∠ACO | |||