学点点

详细内容

疑难解答：

学员在学习中遇到问题，在这里能得到及时的解决。有问题随时提问，老师解答及时，不留学习盲点。有不懂的题目问老师，逐渐养成独立解决问题的能力。

年级

科目

问题描述

提问时间

初二

数学

急

2014-07-03 17:47:23

菁优网

如图：已知∠BAD=∠DAC=10°，AD⊥AE，且AB+AC=BE．则∠B=______

学点点闵老师 2014-07-03 18:00:41

考点：等腰三角形的判定与性质．

专题：探究型．

分析：延长BA到F，使AF=AC，由AB+AC=BE，等量代换可得出AB+AF=BE，而BA+AF=BF，可得出BF=BE，即三角形BEF为等腰三角形，用顶角∠B，利用三角形的内角和定理表示出底角∠F，再由AD与AE垂直，得到∠DAE为直角，又∠BAD=∠DAC=10°，根据平角的定义求出∠FAE=80°，同时由∠DAC=10°，由直角∠DAE-∠DAC求出∠CAE也为81°，可得出∠CAE=∠FAE，再由AF=AC，AE为公共边，利用SAS可得出三角形AFE与三角形ACE全等，根据全等三角形的对应角相等可得出∠F=∠ACE，由∠ACE为三角形ABC的外角，根据外角的性质得到∠ACE=∠B+∠BAC，由∠BAC的度数，表示出∠ACE，即为∠F，根据表示出的∠F相等列出关于∠B的方程，求出方程的解即可得到∠B的度数．

解答：解：延长BA到F，使AF=AC，连接EF，如图所示：
菁优网

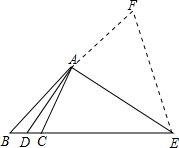∵AB+AC=BE，
∴AB+AF=BE，即BF=BE，
∴∠F=∠BEF=

180°−∠B

，
∵∠BAD=∠DAC=9°，AD⊥AE，即∠DAE=90°，
∴∠FAE=180°-（∠BAD+∠DAE）=180°-（9°+90°）=81°，
∠CAE=∠DAE-∠DAC=90°-9°=81°，
∴∠FAE=∠CAE，
在△AFE和△ACE中，
∵

AF＝AC

∠FAE＝∠CAE

AE＝AE

，
∴△AFE≌△ACE（SAS），
∴∠F=∠ACE，
又∵∠ACE为△ABC的外角，
∴∠ACE=∠B+∠BAC=∠B+18°，
∴∠F=∠B+18°，
∴∠B+18°=

180°−∠B

，
则∠B=48°．
故答案为：48°

点评：此题考查了等腰三角形的判定与性质，全等三角形的判定与性质，三角形的外角性质，以及三角形的内角和定理，利用了转化及等量代换的思想，其中根据题意作出如图所示的辅助线是解本题的关键．

学点点闵老师 2014-07-03 18:02:34

将9度的地方都改为10度。

秦鸿玮 2014-07-03 18:06:18

老师，你顺便帮我u算一下

秦鸿玮 2014-07-03 18:06:26

O(∩_∩)O谢谢了

学点点闵老师 2014-07-03 18:54:40

老师现在在外面，用手机回答不太方便。

学数学不能懒哦，一般都还要求举一反三呢！

你把角度带进去一下很简单的。

该问题已结帖