学点点

详细内容

疑难解答：

学员在学习中遇到问题，在这里能得到及时的解决。有问题随时提问，老师解答及时，不留学习盲点。有不懂的题目问老师，逐渐养成独立解决问题的能力。

年级

科目

问题描述

提问时间

初二

数学

2014-07-02 19:20:06

学点点闵老师 2014-07-02 19:30:27

考点：梯形中位线定理；平行线的性质；三角形内角和定理；等腰三角形的性质．

专题：作图题；探究型．

分析：（1）由两直线平行同旁内角互补，及角平分线的性质不难得出∠1+∠3=90°，再由三角形内角和等于180°，即可得出∠AEB是直角的结论；
（2）过E点作辅助线EF使其平行于AM，由平行线的性质可得出各角之间的关系，进一步求出边之间的关系；
（3）由（2）中得出的结论可知EF为梯形ABCD的中位线，可知无论DC的两端点在AM、BN如何移动，只要DC经过点E，AD+BC的值总为一定值．

解答：解：（1）∵AM∥BN，
∴∠MAB+∠ABN=180°，
又AE，BE分别为∠MAB、∠NBA的平分线，
∴∠1+∠3=

（∠MAB+∠ABN）=90°，
∴∠AEB=180°-∠1-∠3=90°，
即∠AEB为直角；
（2）过E点作辅助线EF使其平行于AM，
∵AM∥BN，EF∥BC，
∴EF∥AD∥BC，
∴∠AEF=∠4，∠BEF=∠2，
∵∠3=∠4，∠1=∠2，
∴∠AEF=∠3，∠BEF=∠1，
∴AF=FE=FB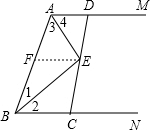，菁优网

∴F为AB的中点，又EF∥AD∥BC，
根据平行线等分线段定理得到E为DC中点，
∴ED=EC；
（3）由（2）中结论可知，无论DC的两端点在AM、BN如何移动，只要DC经过点E，
总满足EF为梯形ABCD中位线的条件，所以总有AD+BC=2EF=AB．

点评：本题是计算与作图相结合的探索．对学生运用作图工具的能力，以及运用直角三角形、等腰三角形性质，三角形内角和定理，及梯形中位线等基础知识解决问题的能力都有较高的要求．

曹毅凯 2014-07-02 19:48:59

老师，实在不好意思，我儿子拍了三次，我以为是三份卷，没有看就发三次了

该问题已结帖