您好，欢迎您来到学点点！
400-678-6991 点击这里给我发消息王老师 点击这里给我发消息丁老师
详细内容
疑难解答：
学员在学习中遇到问题，在这里能得到及时的解决。有问题随时提问，老师解答及时，不留学习盲点。有不懂的题目问老师，逐渐养成独立解决问题的能力。
年级 科目 问题描述 提问时间
初二 数学 数学 2014-07-01 19:48:34
学点点闵老师 2014-07-01 19:55:53
考点：二次函数综合题．
专题：计算题．
分析：分别过B1，B2，B3作y轴的垂线，垂足分别为A、B、C，设A0A1=a，A1A2=b，A2A3=c，则AB1=
3
2
a，BB2=
3
2
b，CB3=
3
2
c，再根据所求正三角形的边长，分别表示B1，B2，B3的纵坐标，逐步代入抛物线y=
2
3
x2中，求a、b、c的值，得出规律．
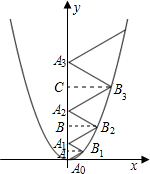解答：菁优网解：分别过B1，B2，B3作y轴的垂线，垂足分别为A、B、C，
设A0A1=a，A1A2=b，A2A3=c，则AB1=
3
2
a，BB2=
3
2
b，CB3=
3
2
c，
在正△A0B1A1中，B1（
3
2
a，
a
2
），
代入y=
2
3
x2中，得
a
2
=
2
3
•（
3
2
a）2，解得a=1，即A0A1=1，
在正△A1B2A2中，B2（
3
2
b，1+
b
2
），
代入y=
2
3
x2中，得1+
b
2
=
2
3
•（
3
2
b）2，解得b=2，即A1A2=2，
在正△A2B3A3中，B3（
3
2
c，3+
c
2
），
代入y=
2
3
x2中，得3+
c
2
=
2
3
•（
3
2
c）2，解得c=3，即A2A3=3，
由此可得△A2009B2010A2010的边长=2010．
故答案为：2010．
点评：本题考查了二次函数的综合运用．关键是根据正三角形的性质表示点的坐标，利用抛物线解析式求正三角形的边长，得到规律．

该问题已结帖
学点点，全国统一客服热线：400-678-6991 客服邮箱：E-mail:xueku51@163.com
版权所有 学点点 Copyright 2015 www.51xuedd.com All rights reserved  ICP证：浙ICP备2023042842号