| 年级 | 科目 | 问题描述 | 提问时间 |
| 初二 | 数学 | 数学 | 2014-07-01 19:27:53 |
 | |||
| 学点点闵老师 2014-07-01 19:41:28 | |||
 证明：三角形的外角和为360°．已知：
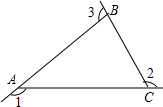
∠1、∠2、∠3为△ABC的三个外角，如图
．求证：
∠1+∠2+∠3=360°
．证明：
考点：三角形内角和定理．
专题：证明题．
分析：根据图形写出已知、求证，然后进行证明：先利用三角形外角性质得到∠1=∠ABC+∠ACB，∠2=∠ABC+∠BAC，∠3=∠ACB+∠BAC，再把它们相加，然后根据三角形内角和可得到∠1+∠2+∠3=360°．
解答：证明：三角形的外角和为360°．
已知：∠1、∠2、∠3为△ABC的三个外角，如图． 求证：∠1+∠2+∠3=360°． 证明：∵∠1是△ABC的外角， ∴∠1=∠ABC+∠ACB， 同理得∠2=∠ABC+∠BAC，∠3=∠ACB+∠BAC， ∴∠1+∠2+∠3=（∠ABC+∠ACB）+（∠ABC+∠BAC）+（∠ACB+∠BAC）， =2（∠ABC+∠ACB+∠BAC） ∵∠ABC+∠ACB+∠BAC=180°， ∴∠1+∠2+∠3=360°． 故答案为∠1、∠2、∠3为△ABC的三个外角，如图；∠1+∠2+∠3=360°． | |||
